| in: Proceedings of the Fourth
Australian Conference on Neural Networks, (ACNN'93),
pages. A:5-8, February 1993
| POSTSCRIPT
|
Unification in Prolog by Connectionist Models
Volker Weber
University of Hamburg,
Computer Science Department,
Natural Language Systems Division
D-2000 Hamburg 50, Bodenstedtstraße 16, Germany
e-mail: weber@nats4.informatik.uni-hamburg.de
Abstract
This paper describes a connectionist unification strategy. We introduce an
uncertainty measure for unification. A self-organizing feature map is used for
learning a similarity measure and a relaxation-network is used for unification.
The coding allows a precise representation of terms. In addition belief-values
may be used to introduce uncertainty. If strict unification without uncertainty
is used, correctness, completeness, and terminating of the method can be
proven. The proof may be seen as a argument for the adequacy of unification
with uncertainty. The system uses linear time in worst case and for
sub-problems of unification, like matching or word-problem, constant time. The
described strategy is able to cope with an extension to unification: It need
not to check whether a variable does refer to the whole of the term (infinite
unification). Unification by this net is very efficient and offers the ability
to cope with uncertain data.
1 Introduction
In general unification is a technique which substitutes variables by adequate
terms to make them equivalent. There is a wide field of applications for
unification like database systems, knowledge acquisition, computer graphics,
natural language processing, expert systems, algebra, deduction- and
rewrite-systems, as well as logic programming [7,
15]. Classical symbolic unification-algorithms
consist of four rules for unification and two for termination. If
t1 and t2 are the terms
to be unified (X variable, t term, f, g
functors, x arbitrary symbol) a system R =
{t1 = t2} is said to
be unifyable if after termination of the algorithm the set R' equals
Ø [4]:
- 1.
- terminating rules (have to be used, if match):
| (f(...) = g(...)) in R
and f ¬ = g
| (CLASH)
|
| (X = t) in R and
X occurs in t
| (OCCURRANCE)
|
- 2.
- unification rules:
(f(t11,..., t1n) =
f(t21,..., t2n)) in R
| ==>
| R' :=
R\(f(t11,..., t1n) =
f(t21,..., t2n)) U
{t11 = t21, ..., t1n = t2n}
| (DECOMPOSITION)
|
| (x=x) in R
| ==>
| R' := R\(x=x)
| (TAUTOLOGY)
|
| (X=t) in R
| ==>
| R' := {{X/t} ð | ð in R}
| (APPLICATION)
|
| (t=X) in R
| ==>
| R' := R\(t=X) U
{X=t}
| (ORIENTATION)
|
After the application of a unification-rule the set R' becomes again
R and the algorithm iterates since R becomes Ø, or a
termination rule has to be used. This rule-system seems to be rather small and
to be computed efficient. Automatical theorem provers, like Prolog, spend often
more than 50% of time for unification. For an efficient computation a skill
selection of unification-rules is needed. Also the occur-check is very
expensive. Some strategies use infinite unification which does not need to
check occurrence.
There are some parallel unification-strategies but the sequential nature of
unification has been shown [3,
20]. Most connectionist approaches implement only
parts of unification. Also, the well known approach of Ballard
[1] belongs to this category. Those of Müller,
Stolcke and Hölldobler [5,
9, 16] implement unification
for different purposes. Their approaches are based on symbolic strategies and
implemented with a high degree of parallelism.
Our approach implements full unification. It is also possible to do infinite
unification. Moreover it is possible to set fuzzy-slots which are basis for the
uncertainty-management. For this it is in addition possible to fuzzy-unify
terms which are similar. The system utilizes therefore a self-organizing
feature-map, a relaxation-net, and a map to determine the mgu (most general
unifier). The weights of the second map are given by the stable relaxation-net.
The system's time-complexity is linear.
2 Representation
In our approach we use a representation similar to that of Hölldobler
[5]. This representation may be called local
cause there is one unit for every constant at every (argument-)position of a
term. On the other hand there is no local coding of every possible term or
every possible substitution (ref. [1]). We represent
terms as follows: Atoms/functors (constants) are represented by a cube of
vectors. Each vector represents one constant. Variables are represented by
variable-vectors. All column-vectors (those of the cube and the
variable-vectors) have the same number of components. Each component of a
vector (or layer of the cube) represents position of a term.
A variable-binding is represented by corresponding activation-patterns of a
variable-vector and a column-vector. For example: In
fig.1 variable Y is bound to constant
a/0. The depicted coding represents the term f(g(a,X)). The
units of the representation are activated with values between 0.0 and 1.0
corresponding to their certainty. A self-organizing feature map is trained
[8] with a symbolic metric to get a order of vectors.
This order represents similarities between constants cause of the symbolic
metric.
3 Training the map
The chosen representation of terms allows us to use uncertainty and
similarities during processing. Similarities between constants are expressed by
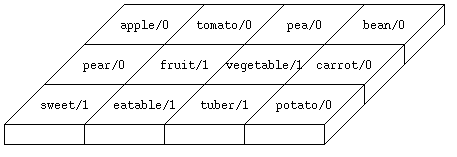
neighborhoods in the feature map. Fig.2 shows the
representation of such similarities for the following predicates:
| fruit(apple). |
fruit(pear). |
| vegetable(tomato). |
vegetable(pea). |
| vegetable(bean). |
vegetable(carrot). |
| tuber(carrot). |
tuber(potato). |
| eatable(X):-fruit(X). |
eatable(X):-vegetable(X). |
| eatable(X):-tuber(X). |
eatable(fruit(X)). |
| sweet(fruit(X)). |
sweet(pear). |
In these predicates there is a similarity between carrot/0 and
potato/0. For both there is a fact tuber(...). This is
represented by a direct neighborhood. The training-vectors for the feature map
are determined as follows: For every occurring constant in a Prolog-system a
vector is generated. This vector contains a component for every occurring
constant. These components contain the number of terms, where the constant it
encodes and the constant the vector encodes occur in common. The vectors are
normalized over all components. Training-vectors are used by the feature map
to find relationships of identical constants between different terms. Such a
coding is adequate since a position in a Prolog-program is often connected to
a distinct meaning. If there are different constants at the same position this
constants are often used in the same context and therefore similar to some
degree. Numbers of similarities between terms can be used to fix similarities
between different constants. Similar constants may be members of one class.
Feature maps are said to reduce high-dimensional dependencies to a
lower-dimensionality conserving many similarities.
4 A hybrid theorem prover
Using the described representation and training of the feature map a hybrid
theorem prover named l-CUP (local Connectionist Unifying Prolog) was
built. It is part of the system CUP [19] containing
several symbolic algorithms and a distributed strategy (d-CUP
[18]). The theorem-prover itself is a symbolic system.
If the system needs to calculate a mgu the currently selected
unification-strategy is invoked.
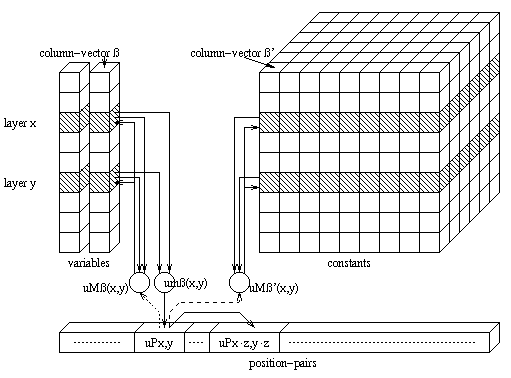
The coding of two terms is presented to a relaxation-net
(fig.3). After relaxation the variable-vectors are
matched into the net to determine the binding. To make use of unification with
uncertainty the units of the representation are initialized to values between
0.0 and 1.0. If uncertainty is used also units in the neighborhood are
initialized. The certainty can be controlled from the symbolic system by fuzzy
slots. A fuzzy slot is defined by the predicate:
cup_fuzzy_slot(Fuzzy variable,
Fuzzy term, Belief). It gives every
term compatible with the fuzzy variable a particular belief-value in a context
which is compatible with the fuzzy term. The system is divided in two phases:
The analysis-phase, where a program has to be analyzed, a coding takes place,
and the system is trained. In the unification-phase the network can be used
during a symbolic-proof.
4.1 Analysis-phase
After the consultation of a Prolog-program the training vectors are encoded and
the relaxation-net (fig.3) is constructed. The map is
trained and the order of the constants is mapped to the column-vectors of the
relaxation-net (fig.1).
4.2 Unification-phase
The unification-step in l-CUP is based on the coding described in
sec.2. Terms to be unified are encoded in the
same net and the same variable-vectors by superposition of activations.
Superposition is done by activating a unit with the maximum of activations. The
relaxation-net computes the weights of a second feature map. Activations of
units of the stable relaxation-net represent weights of the map.
Connection structure of the relaxation-net
Units of components of variable-vectors propagate their activations to the
units of the position-pairs: There is a unit
uPx,y in
the position-pairs for every pair (x, y) of different layers a
unit
uPx,y.
The units of the components x and y of a variable-vector
(ß in V) are connected to a minimum-unit
umß(x,y)
which is connected itself to a unit
uPx,y:
| w |
u |
m |
ß(x,y) |
,u |
(x',ß) |
:= 1, iff (x' in {x, y}) and
(ß in V) |
A minimum-unit
umß(x,y)
is connected to a unit of the position-pairs
uPx,y:
| w |
u |
P |
x,y |
,u |
m |
ß(x',y') |
:= 1, iff (x = x') and
(y = y') |
A unit
uPx,y
indicates, that two positions x and y have to be unified. There
are also connections between units of the position-pairs. Such a connection
exists from a unit
uPx,y to
a unit
uPx.z,y.z
(fig.3):
| w |
u |
P |
x',y' |
,u |
P |
x,y |
:= 1, iff (x' = x.z) and
(y' = y.z) |
For every two components x and y of a column-vector
ß there is a maximum-unit
uMß(x,y).
Every
uMß(x,y)-unit
is connected to the component x of a column-vector ß. The
threshold of
uMß(x,y)
is given by the activation of unit
uPx,y:
| w |
u |
M |
ß(x,y) |
,u |
(x',ß') |
:= 1, iff (x' in {x, y}) and
(ß' = ß) |
| w |
u |
(y',ß') |
,u |
M |
ß(x,y) |
:= 1, iff (y' in {x, y}) and
(ß' = ß) |
In all other cases the units are not connected.
The activation of a component of the column-vector is computed by:
| a |
t+1 |
(u |
(x,ß) |
) := max(w |
u |
(x,ß) |
,u |
M |
ß(x,z) |
* a |
t |
(u |
M |
ß(y,z) |
)) for all y,z. |
This means that the activation of a component x of a column-vector
ß is computed based on the activations of the maximum-units. The
minimum-units, whose activation may be seen as a signal for the same variable
occurring in different positions, have an initial activation of 2. Its
activation is computed from the activations of the corresponding components
x and y of a variable-vector ß:
| a |
t+1 |
(u |
m |
ß(x,y) |
) |
:= |
|
|
| < |
w |
u |
m |
ß(x,y) |
,u |
(x,ß) |
* |
a |
t |
(u |
(x,ß) |
) |
| <= |
w |
u |
m |
ß(x,y) |
,u |
(y,ß) |
* |
a |
t |
(u |
(y,ß) |
) |
|
|
|
| < |
w |
u |
m |
ß(x,y) |
,u |
(y,ß) |
* |
a |
t |
(u |
(y,ß) |
) |
| < |
w |
u |
m |
ß(x,y) |
,u |
(x,ß) |
* |
a |
t |
(u |
(x,ß) |
) |
|
|
The activations of the units of the position-pairs are used as thresholds for
the maximum-units. To prohibit an activation of maximum-units without the
activation of two corresponding units of the variable-vector they are
initialized to 2. The activation of the
uPx,y-unit
decreases if the two corresponding components of the variable-vector
ß are active, or activation from other units of the
position-pairs is propagated:
|
|
| w |
u |
P |
x,y |
,u |
m |
ß(x,y) |
* |
a |
t |
(u |
m |
ß(x,y) |
) |
, |
| w |
u |
P |
x,y |
,u |
P |
x',y' |
* |
a |
t |
(u |
P |
x',y' |
)) |
|
for all ß, x', y' |
The maximum-unit is initialized to 0. Its activation-function is given by:
| w |
u |
M |
ß(x,y) |
,u |
(y',ß) |
* |
|
|
| (y'=x) |
and |
a |
t |
(u |
P |
x,y |
) |
| <= |
w |
u |
M |
ß(x,y) |
,u |
(x,ß) |
* |
a |
t |
(u |
(x,ß) |
) |
| >= |
w |
u |
M |
ß(x,y) |
,u |
(y,ß) |
* |
a |
t |
(u |
(y,ß) |
) |
|
|
|
| (y'=y) |
and |
a |
t |
(u |
P |
x,y |
) |
| <= |
w |
u |
M |
ß(x,y) |
,u |
(y,ß) |
* |
a |
t |
(u |
(y,ß) |
) |
| > |
w |
u |
M |
ß(x,y) |
,u |
(x,ß) |
* |
a |
t |
(u |
(x,ß) |
) |
|
|
This activation-function allows the maximum-unit
uMß(x,y)
to get the maximum of the activation of the units
u(x,ß) and
u(y,ß) if it is above
the activation of the
uPx,y-unit.
The net utilizes a synchron update.
The activation of a unit of the position-pairs changes if two units of a
variable-vector are active, or an activation through the units of the
position-pairs takes place. It follows that the activations of the units of the
position-pairs are changed if the stable state is not reached. Therefore only
the units of the position-pairs have to be tested for a stable state. The
activation of the units of the position-pairs can only decrease or become
stable. Their lowest activity is 0. Therefore the net is at least stable if the
activity of all position-pair-units is 0.
If the net reaches a stable state the variable-vectors are matched through all
column-vectors. Two corresponding vectors indicate a variable-binding. All
variable-bindings form the mgu.
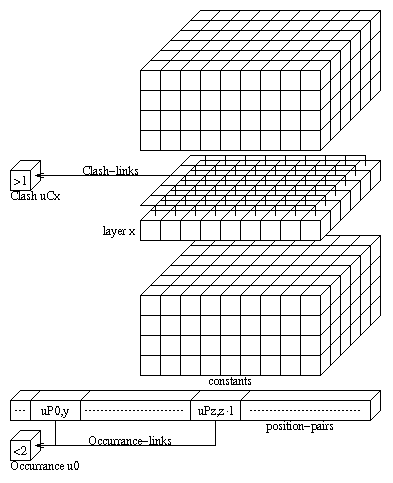
So far it was not mentioned that two terms might not be unifyable. The two
terminating-rules CLASH and
OCCURRENCE are easy to integrate
into the relaxation net. If someone likes to do infinite unification the
OCCURRENCE-unit
uO is not needed. A
CLASH is indicated by an activation which exceeds 1 as the
sum over all units of a layer (fig.4).
OCCURRENCE is determined by activating two units of the
position-pairs, where one decodes an position which represents a sub-term of
the other (fig.4).
The correctness and completeness of the method can be proven by a mapping to
the unification-rules. This is sufficient for a proof cause the correctness and
completness of the unification-rules are proven. We introduce
CLASH- and
OCCURRENCE-units by name. These
units do in fact the same as the corresponding rules. The system needs no
ORIENTATION-rule cause there is
no orientation in the representation. The
DECOMPOSITION-rule may be
found in the representation where the same position in different terms
activates units in the same layer.
TAUTOLOGY is represented by the
activation of the same unit by two different terms and
APPLICATION by activation of
units of a variable-vector and of a column-vectors in the same components. The
method terminates always cause the relaxation-net will reach a stable state. A
detailed proof can be found at Weber [19].
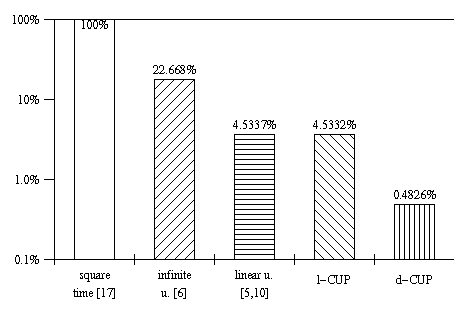
We first tested l-CUP's speed. The results for the time consumption are
based on five different methods. We examined 64,458 unifications during the
proof of queries made with a Prolog-based library-database-system containing
about 7,000 clauses. Fig.5 shows the consumed time for
different unification algorithms in a logarithmically scaled form. 100% for the
square-time method are 26,715,102 unification steps. The result for
d-CUP seems to be better but we should point out that it is a heuristic
which does approximate unification and might fail.
l-CUP is able to do (extended) unification. Among the connectionist
unification methods only Müller, Stolcke and Hölldobler's implement
complete unification [5,
9, 16]. Hölldobler's
method has also the ability to deal with infinite unification but it is not
able to deal with uncertainty.
Stolcke mentioned that activations of a connectionist unification net could be
used as signals for uncertainty [16, p.88]. A similar
idea also appears in Shastri [13, p.339]. The approach
of Stolcke shows the relationship between term-unification, which is done in
Prolog, and unification based grammar formalisms. Natural language processing
grammar formalisms are often used independently from context. Such a method is
syntactically plausible but misses the ability of fault-tolerant analysis.
Rules which introduce semantic information promise to improve this. Such extra
knowledge is often added to grammars by declarative descriptions
[11]. Declarative rules are only capable for
cases which are known. A connectionist method which introduces similarity and
uncertainty to unification might be able to deal with inconsistent, ill-formed
and elliptic input.
As unification has a sequential nature [3] it is
highly unlikely that there is a strict unification method which computes a mgu
in constant time. l-CUP computes the mgu in linear time and belongs
therefore to the fastest unification methods.
6 Conclusion
A connectionist model for unification has been introduced. The model is able
to compute a mgu in linear time and belongs therefore to the fastest
unification methods. The model is able to do infinite unification. Moreover the
ability to deal with uncertainty during unification is given. The use of
uncertainty-unification can be controlled from the hybrid theorem prover. For
this the correctness, terminating, and completeness of the strategy doing
strict unification can be proved. Furthermore such a prove can be seen as a
good argument for the adequacy of the uncertainty-management. Classical methods
do not have a natural equivalence to this option. Such mechanisms could be used
in information retrieval, data base systems or natural language systems.
This work has been partly supported by the ``Deutsche Forschungsgemeinschaft
(DFG-Ha 1026/6-1)''. We also would like to thank R. Hannuschka, U. Hartmann,
M. Mandischer, and S. Wermter for their encourragement.
- 1
-
D. H. Ballard.
Parallel logic inference and energy minimization.
Technical Report TR 142, Computer Science Department, The University of
Rochester, Rochester, NY 14627, March 1986. also published as:
[2].
- 2
-
D. H. Ballard.
Parallel logic inference and energy minimization.
In Proceedings of the fifth National Conference on Artificial
Intelligence (AAAI-86), pp. 203-208. (Philadelphia, PA), 1986.
also published as: [1].
- 3
-
C. Dwork, P. C. Kanellakis, J. C. Mitchell.
On the sequential nature of unification.
Journal of Logic Programming, 1:35--50, 1984.
- 4
-
N. Eisinger, H. J. Ohlbach.
Deduction systems based on resolution.
Technical Report SR-90-12, Universität Kaiserslautern, Fachbereich
Informatik, D-6750 Kaiserslautern, PO-BOX 3049, 1990. (DVI)
- 5
-
S. Hölldobler.
A Connectionist Unification Algorithm.
Technical Report TR-90-012, International Computer Science Institute,
Berkeley, California, March 1990.
- 6
-
G. Huet.
Resolution d'equations dans les langages d'odre 1, 2, ..., w.
PhD thesis, Université de Paris VII, 1976.
- 7
-
K. Knight.
Unification: A multidisciplinary survey.
Computing Surveys, 21(1):93-124, March 1989.
- 8
-
T. Kohonen.
Self-Organization and Associative Memory.
Springer Series in Information Sciences. Springer Verlag, Berlin,
1984.
- 9
-
J. Müller.
Assoziative Prozessoren und ihre Anwendung für das Theorembeweisen.
Master's thesis, Universität Kaiserslautern, 1983.
- 10
-
M. S. Paterson, M. N. Wegman.
Linear unification.
In Proceedings of the Symposium on the Theory of Computing,
1976.
- 11
-
F. C. N. Pereira, S. M. Shieber.
The semantics of grammar formalisms seen as computer languages.
In Proceedings of the 10th International Conference on Computational
Linguistics, pp. 123-129. (Stanford University, Stanford, CA),
July 1984.
also: [14, I:37-58].
- 12
-
J. A. Robinson.
A machine-oriented logic based on the resolution principle.
Journal of the ACM, 12(1):23-41, January 1965.
- 13
-
L. Shastri.
A connectionist approach to knowledge representation and limited inference.
Cognitive Science, 12:331-392, 1988.
- 14
-
S. M. Shieber, F. C. N. Pereira, L. Karttunen, M. Kay.
A compilation of papers on unification-based grammar formalisms.
Technical Report CSLI-86-48, Center for the Study of Language and
Information, Leland Stanford Junior University, April 1986.
- 15
-
J. H. Siekmann.
Unification theory.
Journal of Symbolic Computation, 1989.
- 16
-
A. Stolcke.
Generierung natürlichsprachlicher Sätze in unifikationsbasierten
Grammatiken, Ein konnektionistischer Ansatz.
Master's thesis, Technische Universität München, 1988.
- 17
-
M. Venturini-Zilli.
Complexity of the unification algorithm for first-order expressions.
Technical report, Consiglio Nazionale Delle Ricerche Instituto per le
applicazioni del calcolo, Rome, Italy, 1975.
- 18
-
V. Weber.
Connectionist unification with a
distributed representation.
In International Joint Conference on Neural Networks, IJCNN'92,
vol. III, pp. 555-560, Beijing, China, November 1992.
- 19
-
V. Weber.
Unifikation in Prolog mit konnektionistischen Modellen.
Master's thesis, Universität Dortmund, February 1992.
- 20
-
H. Yasuura.
On the parallel computational complexity of unification.
Technical Report TR-027, ICOT, 10 1983.