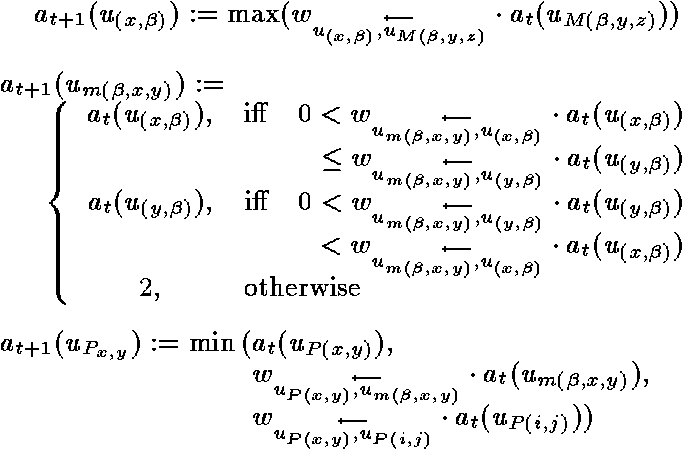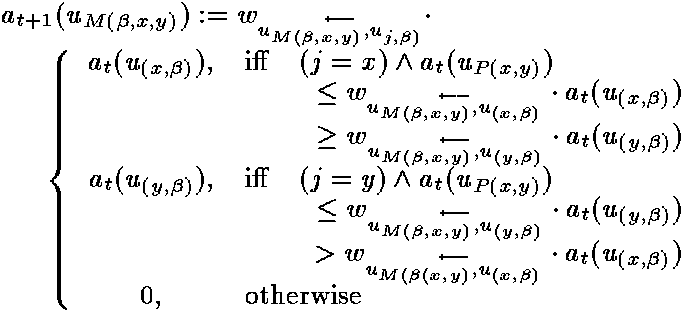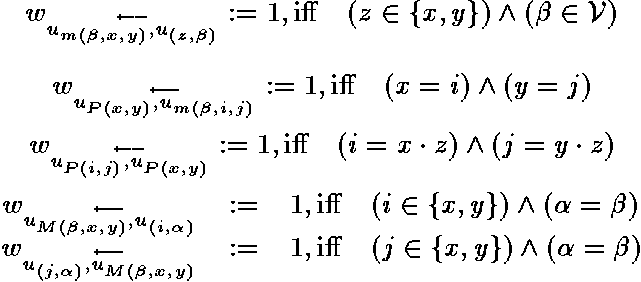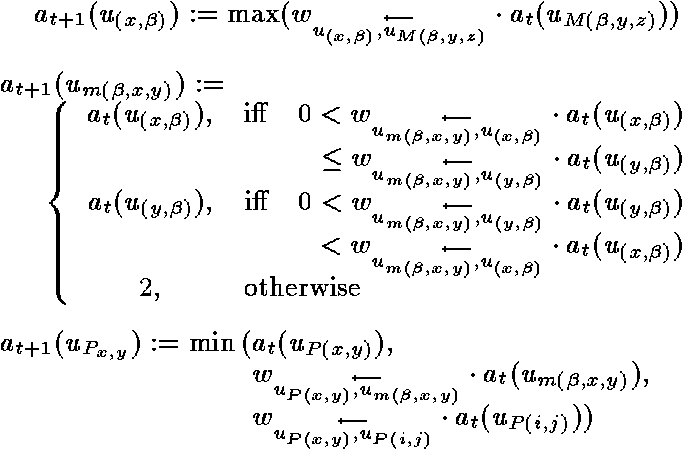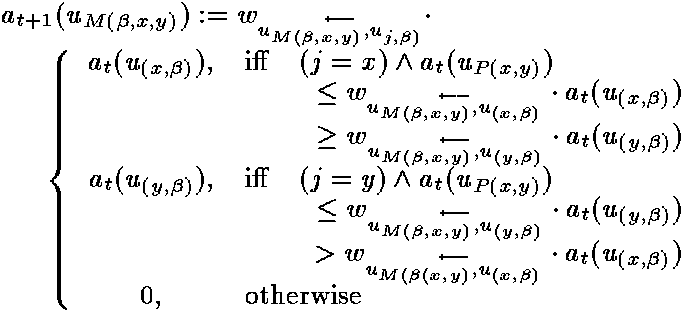| in: R.F.Albrecht, C.R.Reeves and N.C.Steele
(Eds.) Artificial Neural Nets and Genetic Algorithms,
Springer Verlag, Wien, pages. 213-220, April 1993
| POSTSCRIPT
|
Connectionist Unifying Prolog
V. Weber
University of Hamburg,
Computer Science Department,
Natural Language Systems Division
D-2000 Hamburg 50, Bodenstedtstr. 16, Germany
e-mail: weber@nats4.informatik.uni-hamburg.de
Abstract
We introduce an connectionist approach to unification using a local and a
distributed representation. A Prolog-System using these unification-strategies
has been build.
Prolog is a Logic Programming Language which utilizes unification. We introduce
a uncertainty measurement in unification. This
measurement is based on the structure-abilities of the chosen representations.
The strategy using a local representation, called l-CUP, utilizes a
self-organizing feature-map (FM-net) to determine similarities between terms
and induces the representation for a relaxation-network (relax-net). The
strategy using a distributed representation, called d-CUP, embeds a
similarity measurement by its recurrent representation. It has the advantage
that similar terms have a similar representation. The unification itself is
done by a back-propagation network (BP-net).
We have proven the systems adequacy for unification, its efficient computation,
and the ability to do extended unification.
1 Introduction
Unification is generalized matching. It can be seen as the process of
finding unifying substitutions or a unifier:
Mappings like {X <- cat, Y <- cat}
are called substitutions. They can be applied to terms resulting in
objects that differ only in that each variable appearing to the left of an
arrow is replaced by the corresponding term to the right of the arrow.
A unifier for two terms is a set of substitutions whose application to either
of them produces the same result. Thus each of the substitutions above is a
unifier for the terms hairy(X) and hairy(Y). For these two
terms the effect of any unifier can be obtained by first applying the
substitution {X <- Y} and then instantiating further.
We call {X <- Y} a most-general-unifier (or mgu for
short) for hairy(X) and hairy(Y).
There is a wide field of applications for unification like database systems,
knowledge acquisition, computer graphics, natural language processing, expert
systems, algebra, deduction- and rewrite-systems, as well as logic
programming [13].
Classical symbolic unification-algorithms just consist of four rules for
unification and two for termination. If
t1 and
t2 are the terms to be
unified (X variable, t term, f, g functors,
x arbitrary symbol) a system R =
{(t1=t2)}
is said to be unifyable if after termination of the following algorithm the set
R' equals Ø [6]:
- 1.
- terminating rules (have to be used, if match):
| (f(...) = g(...)) in R and
f ¬ = g
| (CLASH)
|
| (X = t) in R and
X occurs in t
| (OCCURRANCE)
|
- 2.
- unification rules:
(f(t11,..., t1n) =
f(t21,..., t2n)) in R
| ==>
| R' :=
R\(f(t11,..., t1n) =
f(t21,..., t2n)) U
{(t11
=
t21),
... ,
(t1n
=
t2n)}
| (DECOMPOSITION)
|
| (x=x) in R
| ==>
| R' := R\(x=x)
| (TAUTOLOGY)
|
| (X=t) in R
| ==>
| R' :=
{{X <- t}S | S in R}
| (APPLICATION)
|
| (t=X) in R
| ==>
| R' := R\(t=X) U
{(X=t)}
| (ORIENTATION)
|
After the application of a unification-rule the set R' becomes again
R and the algorithm iterates since R becomes Ø, or a
termination rule has to be used. This rule-system seems to be rather small
and to be computed efficient. Automatical theorem provers, like Prolog,
however, spend often more than 50% of time for unification. For an efficient
computation a skill selection of unification-rules is needed. Also the
occur-check is very expensive. Some strategies use infinite unification which
does not need to check occurrence.
Herbrand marks the beginning of logic programming with the first prototype of
a unification algorithm [9]. The widest known
algorithm is that of Robinson [24,
25]. This algorithm has a exponential
time-complexity. Boyer and Moore's `structure sharing'-algorithm reduced
space-complexity but time complexity was still as bad as Robinson's
[3]. In 1975 Venturini-Zilli introduced a marker
strategy which reduces time-complexity to O(n ²)
[36]. Huet gave a almost linear algorithm for a
infinite unification strategy (strategy which need not to check occurrence)
[11]. Paterson and Wegman introduced the first linear
strategy [19]. The disadvantage of their method
is a relative complex data-structure which leeds to time consuming computation
in the average case. Later approaches often have time-complexities worse to
their approach in worst case [16]. There are
also some parallel algorithms [8,
37, 41], but the
sequential nature of unification has been shown [5,
41]. Some unification strategies use special hardware
(transputers, unification-coprocessors, Prolog-machines)
[7, 12,
26].
Most connectionist approaches implement only parts of unification. Also, the
well known approach of Ballard [1] belongs to this
category. Those of Müller, Stolcke and Hölldobler
[10, 18,
31] implement unification for different purposes.
Their approaches are based on symbolic strategies and implemented with a high
degree of parallelism.
Our approach implements full unification. It is also possible to use infinite
unification, and other extensions. Moreover it is possible to set fuzzy-slots
which are basis for the uncertainty-management. For this it is in addition
possible to fuzzy-unify (fuzzify) terms which are similar.
We saw the possibility to build a system with
- efficient computation,
- extended unification,
- fuzzification,
- exact, e.g. proveable and
- adequate strategy and representation.
The next section introduces extensions to unification, like
E-unification (unification under a certain equational-theory E)
or fuzzification. Section 3 explains the used
representations. The basic architecture for the overall system is described in
the next section. We will focus on the strategies used by l-CUP and
d-CUP in section 5. There we also
introduce the networks themselves. The results show some experiments with the
system. Before the conclusion we discuss the results and system in comparison
to other approaches.
2 Extended Unification
There exist some extensions to simple unification like the so called
E-unification. E is an equational theory defined by a set of
axioms. It induces the reflexive, transitive and antisymetric congruence
=E on the set of terms. If we have a set of
E-equations {s1
=E
t1, ...,
sn
=E
tn}
than f(s1, ...,
sn)
=E
f(t1, ...,
tn) is E-unifyable.
In such a theory the terms s, t are called E-equal, iff
s =E t. A E-unification
with empty equational theory is called syntactic (kind of unification normally
used in Prolog). A unification with unrestricted equational theory is called
semantic [4]. In Prolog there
are only two terms to be unified. It is, however, possible to unify more than
two terms. The couple of terms to be unified is called an equational-system.
For a E-unification-problem it is necessary to calculate the minimum of
solutions. From this it is possible to get all other unifiers of a
equational-system. A set of unifiers for an equational-system is called
complete, iff every unifier of the equational-system is an instance of one of
its elements. This set is called minimal, iff non of its elements is an
instance of another. There are four unification-classes: Unitary unifying
theories (Uu(E), iff
for every unification-problem exists a minimal complete solution-set),
finite unifying theories
(Uf(E), iff minimal
complete solution-sets exist and this sets are finite), infinite unifying
theories (Ui(E), iff
minimal complete solution-sets exist but there is at least one set which is
infinite) and theories of type zero (U0(E),
iff exists a unification-problem in this theory which does not have a minimal
complete solution-set). Prolog uses a unitary unification.
The unification strategy described in this paper uses another extension to
unification. We call it fuzzification. It was mentioned by Stolcke in 1988 as
fuzzy-unification [31, p.88]. It is a
technique which allows not only strict unification but also unification of
terms which are more or less similar. Therefore a similarity measure has to be
introduced. In symbolic systems someone has to define a similarity criterion
or if we look at fuzzy logic we have to define fuzzy sets and
membership-functions. We make use of the fact that different activations of
units may be seen as a similarity measure for terms. In section
3 we see representations which allow to encode
similarities of constants or terms (figure 1
and 2).
In our approach we control the certainty from the symbolic system by fuzzy
slots. A fuzzy slot is defined by the predicate:
cup_fuzzy_slot(Fuzzy variable,
Fuzzy term,
Belief).
It gives every term compatible with the fuzzy variable a particular
belief-value in a context which is compatible with the fuzzy term. For example:
By cup_fuzzy_slot(X, hunt(X, cat(tom)), low) we set a low
belief-value for the first argument of hunt/2 in the context of
cat(tom). If we think of a data-base were hunt/2 is
ment as hunt(Actor, Recipient) not only a dog could hunt a cat
but in the case of cat(tom) also the mouse jerry
could hunt tom. This is possible, due to fuzzification, even if
no rule or fact for this is in the data-base.
3 Representations
It is necessary to be able to code terms exact, cause unification is a exact
method. Therefore we have to draw special attention to the
representation-problem, cause ''a poor presentation will often doom the model
to failure, and an excessively generous representation may essentially solve
the problem in advance'' [30].
For l-CUP we utilize a representation similar to that of Hölldobler
[10]. This representation may be
called local cause there is one unit for every constant at every
(argument-)position of a term. On the other hand there is no local coding of
every possible term or every possible substitution
(ref. [1]). We represent terms as follows
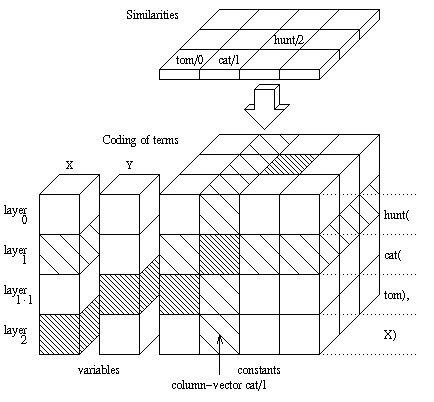
1: Atoms/functors (constants) are represented
by a cube of vectors. Each vector represents one constant. Variables are
represented by variable-vectors. All column-vectors (those of the cube and the
variable-vectors) have the same number of components. Each component of a
vector (or layer of the cube) represents one position of a term.
A variable-binding is represented by corresponding activation-patterns of a
variable-vector and a column-vector. For example: In figure
1 variable Y is bound to constant
tom/0. The depicted coding represents the term
hunt(cat(tom),X). The units of the representation are activated
with values between 0.0 and 1.0 corresponding to their certainty. A FM-net
[14] is trained with a symbolic metric to
get a order of vectors. This order represents similarities between constants
cause of the symbolic metric (see section 5.1.1).
For d-CUP we utilize a representation similar to HRR (Holographic
Reduced Representation [21,
22]. Plate introduced this circular
convolution based representation for short structures, sequences, and
variable-bindings. The convolution-operation given by

 =
=
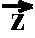 with
with 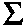 j=0^(n-1) xj * yn-j+i.
There exists now exact inverse of circular convolution. Plate makes use of the
circular correlation - an approximative inverse of circular correlation - which
may be defined as
j=0^(n-1) xj * yn-j+i.
There exists now exact inverse of circular convolution. Plate makes use of the
circular correlation - an approximative inverse of circular correlation - which
may be defined as
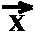

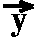 "
(
"
(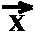 " =
" =
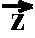 with
zi = xn-i).
We construct a new operation called TCO ( Term Coding
Operation). It is based on HRR and defined for vectors
with
zi = xn-i).
We construct a new operation called TCO ( Term Coding
Operation). It is based on HRR and defined for vectors
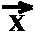 ,
,
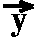 in
[0, 1]^n U
in
[0, 1]^n U
 by
by
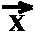
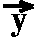 =
2/n(
=
2/n(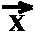
 (
(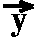

 )),
where ||
)),
where ||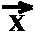 ||L1 =
||
||L1 =
||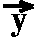 ||L1 = n/2 (||
||L1 = n/2 (||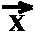 ||Ln =
||Ln =
 ,
,
 =
(n/2 0 0 0 ... 0)). The operation
=
(n/2 0 0 0 ... 0)). The operation
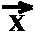

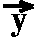 is
defined by the vector addition where every component is divided by 2. For the
TCO we found the exact inverse every time during experiments. An advantage for
representing structured terms is the non-commutativeness of the TCO. This
makes it possible to represent order. Other features which are also advantages
of the HRR as the associativeness and the great influence of a leftmost member
of a sequence for the coding are preserved. Moreover the coding-vectors are all
normalized to the sum of absolutes (L1-norm; n/2). The
coding of a term with TCO is done in the following way:
is
defined by the vector addition where every component is divided by 2. For the
TCO we found the exact inverse every time during experiments. An advantage for
representing structured terms is the non-commutativeness of the TCO. This
makes it possible to represent order. Other features which are also advantages
of the HRR as the associativeness and the great influence of a leftmost member
of a sequence for the coding are preserved. Moreover the coding-vectors are all
normalized to the sum of absolutes (L1-norm; n/2). The
coding of a term with TCO is done in the following way:
- Let f(t1, ..., tm)
be a term (arity m, functor f, arguments
t1, ..., tm),
-
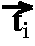 the coding of argument ti, and
the coding of argument ti, and
-
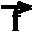 in {0,1},
||
in {0,1},
||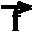 ||L1 = n/2
a coding for the functor.
||L1 = n/2
a coding for the functor.
- The TCO-representation of this term is:
 ...
...
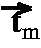 .
.
A coding of the term hunt(cat(tom),X) will be depicted in figure
2.
In our hybrid theorem prover we used vectors
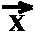 in
{0,1}^n and ||
in
{0,1}^n and ||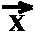 ||L1 = n/2 for the representation of every
constant and variable. With the chosen number of vector-components (32) per
term it is possible to distinguish between (n above n/2) = 601,080,300
constants or variables. The vectors are computed from its internal number by a
hashing-function. They are also decoded by a hashing-function. The local coding
for constants and distributed representations for terms is depicted in figure
2. Circular convolution is done in the
frequence-domain rather than in the time-domain. Therefore we need linear time
for convolution and O(n log n)-time for transformation.
||L1 = n/2 for the representation of every
constant and variable. With the chosen number of vector-components (32) per
term it is possible to distinguish between (n above n/2) = 601,080,300
constants or variables. The vectors are computed from its internal number by a
hashing-function. They are also decoded by a hashing-function. The local coding
for constants and distributed representations for terms is depicted in figure
2. Circular convolution is done in the
frequence-domain rather than in the time-domain. Therefore we need linear time
for convolution and O(n log n)-time for transformation.
4 A hybrid theorem prover
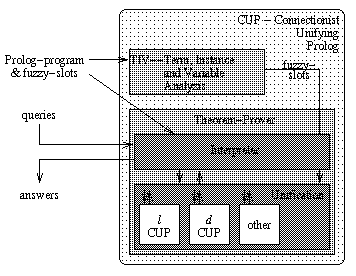
Using the described representations a hybrid theorem prover named CUP
(Connectionist Unifying Prolog) was built. The CUP system contains several
symbolic algorithms, as well as the local l-CUP
[40]) and the distributed strategy
(d-CUP [38]). The theorem-prover
itself is a symbolic system. If the system needs to calculate a mgu the
currently selected unification-strategy is invoked.
The overall-system is depicted in figure 3.
The TIV is used to give all constants of a Prolog-program an internal number
and determine network-sizes. Also fuzzy slots are extracted and coded as real
numbers for fuzzification.
5 Strategies
5.1 l-CUP
The system is divided in two phases: The analysis-phase, where a program has
to be analyzed, a coding takes place, and the system is trained. In the
unification-phase the network can be used during a symbolic-proof.
5.1.1 Analysis Phase
After the consultation of a Prolog-program the training vectors are encoded
and the relax-net (figure 5) is constructed.
The map is trained and the order of the constants is mapped to the
column-vectors of the relax-net (figure 1).
The chosen representation of terms allows us to use uncertainty and
similarities during processing. Similarities between constants are expressed
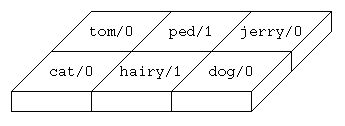
by neighborhoods in the feature map. Figure 4
shows the representation of such similarities for the following predicates:
These predicates induce a similarity between ped/1 and
hairy/1. For both there are facts ...(cat) and
...(dog). This is represented by a direct neighborhood (figure
4). The training-vectors for the FM-net are
significance-vectors and determined as follows: For every occurring constant
in a Prolog-system a vector is generated. This vector contains a component for
every occurring constant. These components contain the number of terms, where
the constant it encodes and the constant the vector encodes occur in common.
The vectors are normalized over all components. Therefore a significance-vector
for ped/1 and our example predicates is:
Training-vectors are used by the FM-net to find relationships between different
terms. Such a coding is adequate since a position in a Prolog-program is often
connected to a distinct meaning. If there are different constants at the same
position this constants are often used in the same context and therefore
similar to some degree. Numbers of similarities between terms can be used to
fix similarities between different constants. Similar constants may be members
of one class. FM-nets are said to reduce high-dimensional dependencies to a
lower-dimensionality conserving many similarities.
5.1.2 Unification Phase
The unification-step in l-CUP is based on the coding described in
section 3. Terms to be unified are encoded in
the same net and the same variable-vectors by superposition of activations.
Superposition is done by activating a unit with the maximum of activations.
The relax-net computes the weights of a second FM-net. Activations of units of
the stable relax-net represent weights of the map.
The coding of two terms is presented to a relax-net (figure
5). After relaxation the variable-vectors are
matched into the net to determine the binding. To make use of unification with
uncertainty the units of the representation are initialized to values between
0.0 and 1.0. If uncertainty is used also units in the neighborhood are
initialized.
Following we present a description of the unit-types. The connection structure
and activation-functions can be found in the appendix and in a paper focusing
on l-CUP [40].
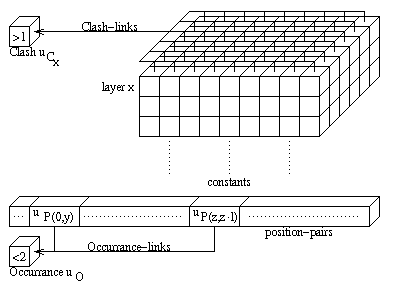
Components of the column-vectors
(u(x,ß)) are activated
if a constant or variable ß occurs on position x. Different
degrees of activations mean different degrees of certainty.
Minimum units
(um(ß,x,y))
receive activation only through the units of the variable vectors
(ß in V). They become active if one variable ß occurs
on two different positions x and y.
The maximum units
(uM(ß,x,y))
are the counterpart of this units. If a variable occurs on two different
positions x and y it is needed to activate all units representing
symbols at position x and y equal. This is done by the maximum
units.
The position-pairs
(uP(x,y))
are needed to control the maximum units. They are also needed to guarantee for
the unification of substructures and have therefore connections between each
other.
The net utilizes a synchronized update.
The activation of a unit of the position-pairs changes if two units of a
variable-vector are active, or an activation through the units of the
position-pairs takes place. It follows that the activations of the units of
the position-pairs are changed if the stable state is not reached. Therefore
only the units of the position-pairs have to be tested for a stable state. The
activation of the units of the position-pairs can only decrease or become
stable. Their lowest activity is 0. Therefore the net is at least stable if
the activity of all position-pair-units is 0.
After reaching the stable state the variable-vectors are matched through all
column-vectors. Two corresponding vectors indicate a variable-binding. All
variable-bindings form the mgu.
So far it was not mentioned that two terms might not be unifyable. The two
terminating-rules CLASH and
OCCURRENCE are easy to
integrate into the relaxation net. For infinite unification the
OCCURRENCE-unit
uO is not needed. A
CLASH is indicated by an activation which exceeds 1 as the
sum over all units of a layer (figure 6).
OCCURRENCE is determined by activating two units of the
position-pairs, where one decodes a position which represents a sub-term of the
other (figure 6).
The correctness and completeness of the method can be proven by a mapping to
the unification-rules. This is sufficient for a proof cause the correctness
and completeness of the unification-rules are proven:
The CLASH- and OCCURRENCE-units do
in fact the same as the corresponding rules. The system needs no
ORIENTATION-rule cause there is
no orientation in the representation. The
DECOMPOSITION-rule may be
found in the representation where the same position in different terms
activates units in the same layer.
TAUTOLOGY is represented by the
activation of the same unit by two different terms and
APPLICATION by activation of
units of a variable-vector and of a column-vector in the same components. The
method terminates always cause the relax-net will reach a stable state. A
detailed proof can be found at Weber [39].
5.2 d-CUP
The system is also divided in two phases: The analysis-phase, where a program
has to be analized, a coding takes place and the system is trained. In the
unification-phase the net can be used during a proof.
5.2.1 Analysis Phase
In the analysis phase the TCO-coding of the data-base takes place (see section
3). We use the PlaNet-simulator
[17] for training and graphical
presentations of term-encodings. For training the unification network is
divided in two parts: the unification problem network
(UPN), and the unification decision problem network
(UDPN; figure 7). The size of the network depends
on the size of the representation for terms.
UPN's output is a suggested mgu, a term with instantiated variables, and for
UDPN a unit for the decision if terms at input are unifyable (figure
7). This unit can be taken as signal for certainty
of unifyability. The observation of the certainty-unit of the network allows to
introduce uncertainty in unification. This can be controlled from the symbolic
system by fuzzy slots which will be compared with the activation of the
certainty-unit. Cause of the ability to represent structures with TCO in a
similarity conserving way it is also possible to unify similar terms.
5.2.2 Unification Phase
The coding is the most important part of d-CUP. The unification step
itself is quite simple. If we have an encoding of two terms and their unbound
variables we can use the trained BP-net to propagate the unifier. After
propagation the mentioned comparison between the certainty-unit and the
fuzzy slots is done. The representation conserves similarities on the symbols
as well as on the connectionist encoding.
It is easy to observe that for the unification rules
TAUTOLOGY,
ORIENTATION and
DECOMPOSITION the
representation is as similar as the symbolic terms if the symbols and the
numerical distances of representations are compared. An encoding that fulfills
this also for the APPLICATION
can not be found. The ground for this is: If we find such a representation
there would be a numerical encoding of the unification and we could test
unifyability of two terms by simple vector-substration in constant time. It is,
however, proven that unification belongs to the hardest problems in P.
If we had found such a representation we would have also found a highly
unlikely result from the complexity view. But we can see that for our purpose
the representation works quite well and the network can be trained.
6 Results
As criteria we want to observe if we are able to fulfill our goals of the
introduction.
For sure it is an obvious criteria to look for the efficiency of computation.
We want to take the time-consumption in dependence of the length of
input-terms. Of course it is necessary to take also the time for (de-)coding.
Also an important factor is the training-time of the BP-net. This time is
difficult to compare with systems which need not to be trained. Therefore we
did not calculate this time. We think our error to this fact is not to big,
cause we have to train the system only once.
It is more difficult to look at the extensions of CUP. If we take the
E-unification as an extension we can compare it to the theoretical
results in unification theory. It is more difficult to rate fuzzification cause
it was not implemented before. Therefore we do not have any comparison. It
seems, however, to be useful to take the degree we are able to control
fuzziness as a criteria for our system. A system that is not able to do strict
unification is worthless.
Beside unification we can have a deep view to the representation. As seen in
section 3 we can show similarity between
representation and symbols with respect to
TAUTOLOGY,
ORIENTATION and
DECOMPOSITION (and in
l-CUP also for
APPLICATION). The similarity
between representations is for d-CUP also independent from the
unification method.
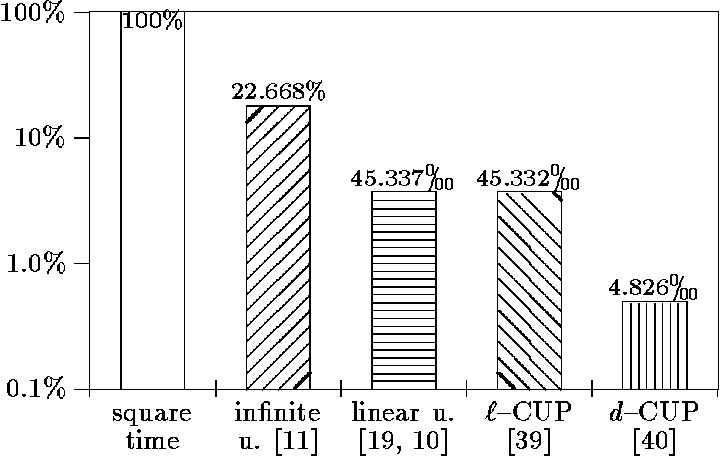
We first tested CUP's speed. The results for the time consumption are based on
five different methods. We examined 64,458 unifications during the proof of
queries made with a Prolog-based library-database-system containing about 7,000
clauses. Figure 8 shows the consumed time for
different unification algorithms in a logarithmically scaled form.
100% for the square-time method are 26,715,102 unification steps. The result
for d-CUP is of course better than l-CUP but we should remark
that d-CUP approximates unification. On the other hand d-CUP did
right on every unification during tests.
We examined several E-unification problems which are based on the axioms
in table 1.
| A |
|
f(f(x, y), z) |
= |
f(x, f(y, z)) |
|---|
| C |
|
f(x, y) |
= |
f(y, x) |
|---|
| D |
DR |
f(x, g(y, z)) |
= |
g(f(x, y), f(x, z)) |
|---|
| |
DL |
f(g(z, y), z) |
= |
g(f(x, z), f(y, z)) |
|---|
Table 1: E-equations for Associativity, Commutativity, and (left & right) Distributivity |
Table 2 gives an overview over the
equational-theories which derive out of this axioms. Some of these theories
are decidable some are undecidable. The theories fall in the three classes
Uu(E),
Ui(E) and
Uf(E). If the theory
is undecidable there exists no terminating algorithm which decides if at least
one admissible unifier exists for this equational-theory. For this theories a
heuristic which approximates the decision is useful. A disadvantage is that
there are some theories which are not unitary like the Prolog-unification. CUP
is designed for unitary unification and will compute for every theory only one
unifier. This unifier seems to be calculated like a syntactic unifier.
Concluding it can be said that CUP is able to do unification and to represent
and interpret similarities in a problem-adequate way. Moreover, as discussed
in an earlier paper, the representation is very robust
[38]. The system is also able to do extended
unifications like E-unification or infinite unification.
7 Discussion
CUP is, as mentioned, able to do (extended) unification. Among the
connectionist unification methods only Müller, Stolcke and Hölldobler
implement complete unification [10,
18,
31].
Hölldobler's method has also the ability to deal with infinite unification
but it is not able to deal with uncertainty.
Stolcke mentioned that activations of a connectionist unification net
could be used as signals for uncertainty
[31, p.88]. A similar idea also appears in
Shastri [27, p.339]. The approach of
Stolcke shows the relationship between term-unification, which is done in
Prolog, and unification based grammar formalisms. Natural language processing
grammar formalisms are often used independently from context. Such a method is
syntactically plausible but misses the ability of fault-tolerant analysis.
Rules which introduce semantic information promise to improve this. Such extra
knowledge is often added to grammars by declarative descriptions
[20]. Declarative rules are only
capable for cases which are known.
As unification has a sequential nature
[5] it is highly unlikely that there is
a strict unification method which computes a mgu, like d-CUP, in
constant time. l-CUP computes the mgu in linear time and belongs
therefore to the fastest -- exact -- unification methods.
D-CUP opens the possibility of fast fault-tolerant computation which
also uses context and similarities of structures.
As mentioned in section 5 there are
several hardware implementations of unification strategies. Several of this
systems have a simple unification-concept. They try to reduce the unification
to other, cheaper methods, like term-matching. Often a type-hierarchy of
arguments is introduced during compilation. D-CUP uses a strategy
similar to matching. Similarities between term-codings are used to get
something like unification. Also Stolcke and Wu developed a distributed
approach to do term-matching [32].
Classical symbolic methods distinguish between different unification-rules.
Such rule-based methods can only seldom be found in distributed connectionist
systems. For l-CUP we compared rules and units while talking about a
proof of the correctness (section
5.1.2). The units and network
of d-CUP can not be divided in parts which realize this rules. But as we
look on the similarity relation and the explanation for its adequacy for this
aim we used this rules.
8 Conclusion
Connectionists models for unification has been introduced. The models are able
to compute a mgu in linear time/approximate the mgu in constant time and belong
therefore to the fastest unification methods. The models are able to do
infinite unification. Moreover the ability to deal with uncertainty during
unification is given. The use of fuzzification can be controlled from the
hybrid theorem prover. For l-CUP the correctness, terminating, and
completeness of the strategy doing unification can be proved. Furthermore such
a prove can be seen as a good argument for the adequacy of the
uncertainty-management. Classical methods do not have a natural equivalence to
fuzzification. Such mechanisms could be used in information retrieval, data
base systems or natural language systems.
Acknowledgements
This work has been partly supported by the German Research Community
(``Deutsche Forschungs-Gemeinschaft; grant DFG-Ha 1026/6-1)''. We also would
like to thank R. Hannuschka, U. Hartmann, H. Wache, and St. Wermter for their
encouragement.
References
- 1
-
D.H.Ballard.
Parallel logic inference and energy minimization.
Technical Report TR 142, Computer Science Department, The University
of Rochester, Rochester, NY 14627, Mar. 1986.
[2].
- 2
-
D.H.Ballard.
Parallel logic inference and energy minimization.
In Proceedings of the 5th National Conference on Artificial
Intelligence (AAAI-86), pages 203--208. (Philadelphia, PA), 1986.
[1].
- 3
-
R.S.Boyer and J.S.Moore.
The sharing of structure in theorem-proving programs.
Machine Intelligence, 7:101--116, 1972.
- 4
-
N.Dershowitz and J.-P.Jouannaud.
Rewrite systems.
In J. van Leeuven, editor, Handbook of Theoretical Computer
Science B: Formal Methods and Semantics, chapter 6, pages 243--320.
North-Holland, Amsterdam, 1990.
- 5
-
C.Dwork, P.C.Kanellakis, and J.C.Mitchell.
On the sequential nature of unification.
Journal of Logic Programming, 1:35--50, 1984.
- 6
-
N.Eisinger and H.J.Ohlbach.
Deduction systems based on resolution.
Technical Report SR-90-12, Universität Kaiserslautern, Fachbereich
Informatik, D-6750 Kaiserslautern, PO-BOX 3049, 1990. (DVI)
- 7
-
J.Hager and M.Moser.
An approach to parallel unification using transputers.
In Proceedings of the 12th German Workshop on Artificial
Intelligence, pages 83--91, 1989.
- 8
-
J.Harland and J.Jaffar.
On parallel unification for Prolog.
New Generation Computing, 5:259--279, 1987.
- 9
-
J.Herbrand.
Recherches sour la théorie de la démonstration.
Travaux de la Soc. des Science et des Lettres de Varsovie,
33(128), 1930.
- 10
-
S.Hölldobler.
A Connectionist Unification Algorithm.
Technical Report TR-90-012, International Computer Science Institute,
Berkeley, California, Mar. 1990.
- 11
-
G.Huet.
Resolution d'equations dans les langages d'odre 1, 2, ..., w.
PhD thesis, Université de Paris VII, 1976.
- 12
-
Y.Kaneda, N.Tamura, K.Wada, H.Matsuda, S.Kuo, and S.Maekawa.
Sequential Prolog machine PEK.
New Generation Computing, 4:51--66, 1986.
- 13
-
K.Knight.
Unification: A multidisciplinary survey.
Computing Surveys, 21(1):93--124, Mar. 1989.
- 14
-
T.Kohonen.
Self-Organization and Associative Memory.
Springer Series in Information Sciences. Springer Verlag, Berlin,
1984.
- 15
-
M.Livesey and J.Siekmann.
Termination and decidability results for string unification.
Technical Report Memo CSM-12, Computing Center, Essex University,
1975.
- 16
-
A.Martelli and U.Montanari.
An efficient unification algorithm.
ACM Transactions on Programming Languages and Systems,
4(2):258--282, Apr. 1982.
- 17
-
Y.Miyata.
A User's Guide to PlaNet Version 5.6 : A Tool for
Constructing, Running, and Looking into a PDP Network.
Department of Computerscience, University of Colorado, Boulder,
version 5.6 edition, Jan. 1991.
- 18
-
J.Müller.
Assoziative Prozessoren und ihre Anwendung für das
Theorembeweisen.
Master's thesis, Universität Kaiserslautern, 1983.
- 19
-
M.S.Paterson and M.N.Wegman.
Linear unification.
In Proceedings of the Symposium on the Theory of Computing,
1976.
- 20
-
F.C.N.Pereira and S.M.Shieber.
The semantics of grammar formalisms seen as computer languages.
In Proceedings of the 10th International Conference on
Computational Linguistics, pages 123--129. (Stanford University, Stanford,
CA), July 1984.
[28, I:37-58].
- 21
-
T.A.Plate.
Holographic reduced representations.
Technical Report CRG-TR-91-1, Department of Computer Science,
University of Toronto, Toronto, Ontario, Canada, May 1991.
- 22
-
T.A.Plate.
Holographic recurrent networks.
In C.L.Giles, S.J.Hanson, and J.D.Cowan, editors, Advances
in Neural Information Processing Systems 5, San Mateo, CA, 1993. (1992),
Morgan Kaufmann.
- 23
-
G.D.Plotkin.
Building in equational theories.
Machine Intelligence, 7:73--90, 1972.
- 24
-
J.A.Robinson.
A machine-oriented logic based on the resolution principle.
Journal of the ACM, 12(1):23--41, Jan. 1965.
- 25
-
J.A.Robinson.
Computational logic: The unification computation.
Machine Intelligence, 6:63--72, 1971.
- 26
-
P.Robinson.
The SUM: An AI coprocessor.
Byte, 10(6):169--180, June 1985.
- 27
-
L.Shastri.
A connectionist approach to knowledge representation and limited
inference.
Cognitive Science, 12:331--392, 1988.
- 28
-
S.M.Shieber, F.C.N.Pereira, L.Karttunen, and M.Kay.
A compilation of papers on unification-based grammar formalisms.
Technical Report CSLI-86-48, Center for the Study of Language and
Information, Leland Stanford Junior University, Apr. 1986.
- 29
-
J.Siekmann.
Unification of commutative terms.
Technical Report IB 2/76, Institut für Informatik I, Universität
Karlsruhe, 1976.
- 30
-
P.Smolensky.
On variable binding and the representation of symbolic structures in
connectionist systems.
Technical Report CU-CS-355-87, Department of Computer Science &
Institute of Cognitive Science, University of Colorado, Boulder (CO), Feb.
1987.
- 31
-
A.Stolcke.
Generierung natürlichsprachlicher Sätze in unifikationsbasierten
Grammatiken, Ein konnektionistischer Ansatz.
Master's thesis, Technische Universität München, 1988.
- 32
-
A.Stolcke and D.Wu.
Tree matching with recursive distributed representations.
Technical Report TR-92-025, International Computer Science Institute,
Berkeley, California, Apr. 1992.
Paper to be represented at the Workshop on Integrating Neural
and Symbolic Processes -- the Cognitive Dimension at the National Conference
on Artificial Intelligence, San Jose, CA, July 1992.
- 33
-
P.Szabó.
The undecidability of the Da-unification problem.
Internal Report IB 04/78, Institut für Informatik I, Universität
Karlsruhe, Karlsruhe, PO BOX 6380, 1978.
- 34
-
P.Szabó.
Theory of First Order Unification.
PhD thesis, Universität Karlsruhe, 1982.
- 35
-
P.Szabó and E.Unvericht.
The unification problem for distributive terms.
Internal Report IB 13/78, Institut für Informatik I, Universität
Karlsruhe, Karlsruhe, PO BOX 6380, 1978.
- 36
-
M.Venturini-Zilli.
Complexity of the unification algorithm for first-order expressions.
Technical report, Consiglio Nazionale Delle Ricerche Instituto per le
applicazioni del calcolo, Rome, Italy, 1975.
- 37
-
J.S.Vitter and R.A.Simons.
Parallel algorithms for unification and other complete problems in P.
In Proceedings of the ACM 1984 Annual Conference: The Fifth
Generation Challange, San Francisco, CA, Oct. 1984.
- 38
-
V.Weber.
Connectionist unification with a distributed representation.
In International Joint Conference on Neural Networks, IJCNN'92,
volume III, pages 555--560, Beijing, China, Nov. 1992. INNS, CNNC, and IEEE
NNC.
- 39
-
V.Weber.
Unifikation in Prolog mit konnektionistischen Modellen.
Master's thesis, Universität Dortmund, Feb. 1992.
- 40
-
V.Weber.
Unification in Prolog by connectionist models.
In Proceedings of the Fourth Australian Conference on Neural
Networks, ACNN'93, pages A:5--8, Sidney, Feb. 1993. (Melbourne, Australia),
SEDAL, University of Sydney Electrical Engineering.
- 41
-
H.Yasuura.
On the parallel computational complexity of unification.
Technical Report TR-027, ICOT, Oct. 1983.
Appendix
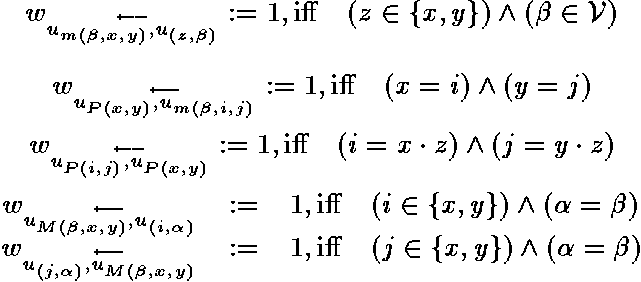
In all other cases the units are not connected.